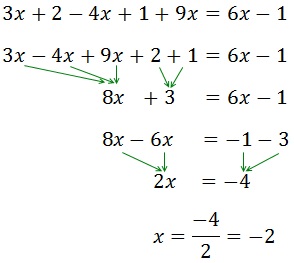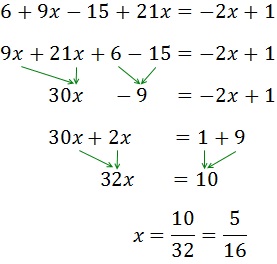Dau virtual. Aquí.
Projectes de Matemàtiques del curs. Aquí.
Vídeos dels temes que farem. Aquí.
Mates 2n tutorial 3r T
SEGON TRIMESTRE
Tema 4. Equacions
Jocs matemàtics:
SEGON TRIMESTRE
Índex:
1. Probabilitat.
2. Equacions càlcul.
3. Equacions problemes.
4. Funcions.
PROJECTE DE PROBABILITAT. Vés a:
Tema 4. Equacions
Jocs matemàtics:
Equacions online:
4 en ratlla:
Bingo equacions:
Puzzle blanc:
http://mates.aomatos.com/puzzles-blancos-para-trabajar-el-algebra/
Tema 5. Problemes d'equacions
😊 Repàs. Problemes amb solucions.
Problemes amb solució i procediment. Aquí. Fes-los a partir del problema 7.
Problemes amb solució i procediment. Aquí. Fes els problemes del "tipus" que hem fet a classe.
Pre-examen
1) La suma de 3 nombres consecutius és 222. Quins són aquests nombres? R: x= 73
2) La suma de 2 nombres consecutius és 57. Quins són aquests nombres? R: x= 28
3) La Paula té 1500 euros. En dóna una quantitat al Marc, el doble d'aquesta quantitat a la Judith i el triple del que ha donat al Marc, li dóna a l'Ethan. Quants diners dóna a cadascú? R: x= 250
4) L'Aleix té 224 sugus i en dóna una quantitat a l'Ainhoa i el triple d'aquesta quantitat al David i la Vlada. Quants en dóna a cadascú? R: x= 56
5) Si a un nombre que no saps li sumes el seu triple i li restes 25 obtens 95. Quin nombre és? R: x= 30
6) Si a un nombre que no saps li sumes la seva meitat i li sumes el seu nombre anterior, et dóna 99. Quin és aquest nombre. R: x= 40
Per preparar l'examen sobre problemes d'equacions
La "xuleta" i els "problemes inventats" els has de portar el dia de l'examen, juntament amb el dossier d'equacions.
Prepararem l'examen en parelles. Indica si ets professor o alumne i el nom del teu professor o alumne.
PROBLEMES D'EQUACIONS DE GEOMETRIA. Tipus 1
Inventa't l'enunciat per a cadascuna d'aquestes equacions.
Exemple:
Problema 1)
1. Equació:
x + x + x + x = 40
2. Resolem l'equació:
4x = 40
4 · x = 40
x= 40/4
x =10 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un quadrat mesura 40 cm. Quant mesura cada costat?
4. Escric la resposta del problema amb una frase i unitats.
Problema 5)
Fes els 4 passos amb la informació que se't dóna.
1. Equació:
x + x+1 + x+2 = 33
" El perímetre d'un triangle escalè (3 costats diferents) mesura 33 cm. Quant valen els 3 costats diferents d'un triangle escalè, sabent que el costat mitjà és 1 cm major que el petit, i el costat gran és 2 cm major que el costat petit".
Indica al dibuix el costat petit (x) el costat mitjà (x+1) i el costat gran (x+2)
Avui. Exercici de classe amb apunts
Passos: 1) Equació 2) Dibuix de la figura amb les "x" i dades 3) Resolem l'equació 4) Resposta amb una frase.
MODEL. NO ES COPIA.
1) Quant mesuren els costat d'un quadrat de 2 cm de perímetre?
1) x+x +x +x=2
2)
3) x+x +x +x=2
4x =2
x=2/4
x=0,5 cm
4) Cada costat del quadrat mesura 0,5 cm.
1) Quant mesuren els costats d'un quadrat de perímetre 320 cm? R: 80 cm.
2) Quant mesuren els costat d'un triangle equilàter de perímetre 24 cm? R: 8 cm.
3) El costat llarg d'un rectangle mesura el triple que el curt. Quant mesura cada costat si el perímetre val 160 m? R:20 curt. R:60 llarg.
4) En un triangle isòsceles (2 costats iguals i 1 de diferent), els dos costats llargs fan el quàdruple (multiplicat per 4 ;-)) que el costat curt. Si el perímetre mesura 90 cm, quant mesuren els costats? R: 10 cm curt. 40 cm els llargs.
5) En un triangle escalè (tots els costats diferents), el costat mitjà mesura 5 cm més que el costat curt. El costat gran mesura 10 cm més que el costat curt. Si el perímetre és 75 cm, quant mesura cada costat? R: Equació: x+ x+5 + x+10 = 75. Costats: 20 cm, 25 cm, 30 cm.
6) Inventa't un problema similar amb un pentàgon o hexàgon. (si et sobra temps)
CORRECCIÓ
1) Quant mesuren els costats d'un quadrat de perímetre 320 cm? R: 80 cm.
x + x + x + x = 320
4x=320
4·x=320
x=320/4
x=80 cm
R: Cada costat fa 80 cm. La resposta és coherent perquè 80 x 4 dóna 320 cm.
2) Quant mesuren els costat d'un triangle equilàter de perímetre 24 cm? R: 8 cm.
x + x + x = 24
3x=24
3·x=24
x=24/3
x=8 cm
R. Cada costat fa 8 cm. La resposta és coherent perquè 8 x 3 dóna 24 cm.
3) El costat llarg d'un rectangle mesura el triple que el curt. Quant mesura cada costat si el perímetre val 160 m? R:20 curt. R:60 llarg.
3x + 3x + x + x = 160
8x=160
8·x=160
x=160/8
x=20 cm
R. El costat curt mesura 20 cm i el llarg 60 cm. Costa. La resposta és coherent perquè si sumes tots els costats dóna 60 + 60 + 20 + 20 = 160 cm.
4) En un triangle isòsceles (2 costats iguals i 1 de diferent), els dos costats llargs fan el quàdruple (multiplicat per 4 ;-)) que el costat curt. Si el perímetre mesura 90 cm, quant mesuren els costats? R: 10 cm curt. 40 cm els llargs.
x + 4x + 4x = 90
9x=90
9·x=90
x = 90/9
x=10 cm
R. Costat curt 10 cm. Costat llarg 40 cm.. La resposta és coherent perquè si sumes els costats (10 + 40 + 40) dóna 90.
5) En un triangle escalè (tots els costats diferents), el costat mitjà mesura 5 cm més que el costat curt. El costat gran mesura 10 cm més que el costat curt. Si el perímetre és 75 cm, quant mesura cada costat? R: Equació: x+ x+5 + x+10 = 75. Costats: 20 cm, 25 cm, 30 cm.
x + x+5 + x+10 = 75
3x + 15 =75
3x =75 - 15
3x = 60
3·x = 60
x=60/3
x=20 cm
R. El costat curt fa 20 cm, el mitjà 25 cm i el llarg 30 cm.. La resposta és coherent perquè si sumes els costats (20 + 25 + 30) dóna 75 cm.
6) Inventa't un problema similar amb un pentàgon o hexàgon. (si et sobra temps)
PROBLEMES DE NOMBRES. Tipus 2
Fes correspondre cada enunciat amb la seva equació. Després resol el problema amb els 4 passos.
Enunciats:
1. Si multipliques un nombre que no saps per 5 i li restes 40 obtens 25. Quin és aquest nombre? (El nombre és la "x").
2. Si a un nombre natural (x) li sumes l'anterior (x-1) i després li sumes el nombre següent (x+1), obtens 111. Quin és el nombre natural?
3. Si a un nombre (x) li sumes la tercera part (x/3) i després li sumes 5, obtens 21. Quin és aquest nombre (x)?
4. Si a 15 li restem el doble d'un nombre que no conec (2x), obtinc 1. Quin és aquest nombre?
Equacions:
A. 15 - 2x = 1 Solució : x= 7
B. x + x/3 + 5 = 21 Solució : x= 12
C. x + (x-1) + (x+1) = 111 Solució : x= 37
D. 5x - 40 = 25 Solució : x= 13
Solucionari:
1. Si multipliques un nombre que no saps per 5 i li restes 40 obtens 25. Quin és aquest nombre? (El nombre és la "x").
D. 5x - 40 = 25 Solució : x= 13
2. Si a un nombre natural (x) li sumes l'anterior (x-1) i després li sumes el nombre següent (x+1), obtens 111. Quin és el nombre natural?
C. x + (x-1) + (x+1) = 111 Solució : x= 37
3. Si a un nombre (x) li sumes la tercera part (x/3) i després li sumes 5, obtens 21. Quin és aquest nombre (x)?
B. x + x/3 + 5 = 21 Solució : x= 12
4. Si a 15 li restem el doble d'un nombre que no conec (2x), obtinc 1. Quin és aquest nombre?
A. 15 - 2x = 1 Solució : x= 7
PROBLEMES DE REPARTIR QUANTITATS. Tipus 3
Exemple 1
1) Equació: x + 2x +3x = 240
2) Resolem l'equació:
x + 2x +3x = 240
6x = 240
x = 240/6
x = 40
3) Enunciat. El Pau té 240 € i en dona una quantitat a l'Aleix. Dóna el doble d'aquesta quantitat a la Maria i el triple d'aquesta quantitat al Pere. Quants diners dona a cadascú?
4) Resposta i reflexió del resultat. Aleix 40 €, Maria 80 € i Pere120 €. És correcta perquè si sumes aquestes quantitats dóna 240 €.
Exemple 2
1) Equació: x + 3x +2 · 3x = 500
x + 3x +6x = 500
2) Resolem l'equació:
x + 3x +6x = 500
10x = 500
x = 500/10
x = 50
3) Enunciat. Reparteixes 500 € i en dones una quantitat a la Paula, el triple del que dones a la Paula ho dones a l'Eric i el doble del que dones a l'Eric ho dones a la Judith (2 · 3x). Quant tindrà cadascú?
4) Resposta i reflexió del resultat. Paula 50€. Eric 150€. Judith 300€. Tot sumat dóna 500 €.
Exemple 3
1) Equació: x + x+ 50 + x + 500 = 670
2) Resolem l'equació:
x + x+ 50 + x + 500 = 670
3x + 550 = 670
3x = 670 - 550
3x = 120
x = 120 / 3
x= 40
3) Enunciat. El Manel té uns diners que no sabem. El Pol té els diners del Manel més 50 €. L'Emma té els diners del Manel més 500 €. Si en total tenen 670 euros, quants diners té cadascú?
4) Resposta i reflexió del resultat. Manel 40 €. Pol 90 €. Emma 540 €. Tot sumat dóna 670 €.
PROBLEMES DE NOMBRES CONSECUTIUS. Tipus 4
Exemple 1
1) Equació: x + x + 1 + x + 2 = 63
2) Resolem l'equació:
x + x + 1 + x + 2 = 63
3x + 3 = 63
3x = 63 - 3
3x= 60
x = 60/3
x = 20
3) Enunciat. La suma de 3 nombres consecutius dóna 63. Quins són aquests nombres?
4) Resposta i reflexió del resultat. Són 20, 21 i 22 perquè sumats donen 63.
Exemple 2
1) Equació: x + x + 1 = 251
2) Resolem l'equació:
x + x + 1 = 251
2x + 1 = 251
2x = 251 - 1
2x = 250
x = 250/2
x = 125
3) Enunciat. La suma de 2 nombres consecutius dóna 251. Quins són aquests nombres?
4) Resposta i reflexió del resultat. Són 125 i 126 perquè sumats donen 251.
Ara ho faig jo:
Inventa't 4 problemes de nombres consecutius. Escriu: 1) Enunciat 2) Equació i resolució de l'equació 3) Resultat i reflexió sobre el resultat.
FUNCIONS
Resultats de l'examen per fer la correcció:
1) 3 euros i 8 euros. 2) 23 euros. 3) 9,9 euros 4) t= (c-3)/0,05 5) 580 minuts
6) 9,6 hores / 9 hores 39 minuts 7) 1r gràfic 8) 540 $ i 860 $ 9) 620 $ 10) V= (M+180)/8
11) 109,43 mph 12) 32 F i 86 F 13) 77 F 14) C= (5F-160) / 9 15) 10 ºC
16) Laia ªF i Jordi ºC 17) 56,07 euros 18) 69 $ 19) opció b)
CÀLCUL AMB FÓRMULES
Exercici 1)
2.1) Funció 1. M = 7V - 170 (Multa= 7· Velocitat - 170) multa en dòlars i velocitat en milles per hora (mph)
2.2) Funció 1. M = 8V - 180 (Multa= 8· Velocitat - 180) multa en dòlars i velocitat en milles per hora (mph)
Joc de cartes
Tablero de ecuaciones
Resoldre equacions online
Symbolab https://es.symbolab.com/solver/linear-equation-calculator/
App mòbil per comprovar el resultat de les equacions:
PhotoMath (Android i IOS)
MalMath (Android)
REPÀS 18/12/2019
Resol i fes l'autocorrecció amb les respostes.
1) x + 1 = 3
2) x - 1 = -5
3) 2x = 16
4) x/6 = 13
5) 2x + x - 5x + 4x = 5 + 4 - 2 + 1
6) x - 1 + 4 - 2x =2x + 8 - 5x + 3
7) x=3 és resultat de l'equació següent? Fes un procediment matemàtic i escriu una frase amb la resposta:
2x + 5 = x - 4
Pista:
2·3 +5 = 3-4
6 + 5 =-1
11 =-1
11 no és igual a -1. Per tant, x=3 no és solució de l'equació.
8) 2 ·(3x+5) = 5
9) -3 (-x +2)= -9
10) -3 ·(2x-1) = -2 ·(-6x-4)
11) Repassa els problemes de fraccions de la fotocòpia i de ONMAT.
Fes el següent llistat d'equacions. Comprova el resultat aquí i posa't la nota:
https://es.symbolab.com/solver/linear-equation-calculator
Fes aquestes equacions i posa't la nota.
1) 2 · ( x + 1) = 5 R: x=3/2
2) 5x + 3 - x = 2x + 7 - x R: x=4/3
3) 4x + 3 - 5x = 3 · (x-1) R: x = 3/2
4) 4 · (x-1) + 2x = 5 - ( x - 3) R: x = 12/7
5) 2x + 3 - 5 = 5x + 4 -2x R: x= - 6
6) x + 3 · (x-1) = 6 + 2 · (x+1) R: x = 11/2
7) x + 5 = 2x + 4 - 5x R: x= -1/4
8) -2 · ( x - 1) = -3 · (x + 1 ) R: x= - 5
9) -5 · ( - x + 1 ) = -3 · (x - 1 ) R: x= 1
10) 2x - 4 · (x - 2 ) = 5x + 1 - 3 · (x+1) R: x=5/2
Repàs:
1) Fes aquestes 10 equacions. Fes l'autocorrecció. Posa't nota.
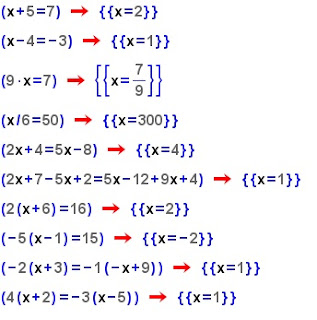
2) Comprova el resultat de l'equació 5, 6, 9 i 10.
3) Has de saber resoldre equacions per deducció.
4) Exercici de "pensar".
A primària ja feies equacions... ;-)
1) Els cotxes que té el Xavi més 5 són 8 cotxes. Quants cotxes té el Xavi?
? + 5 = 8 Resposta: 3 cotxes
2) Si a un nombre li resto 3 obtinc -5. Quin nombre és?
? - 3 = -5 Resposta: -2
3) Els CDs que té l'Íker multiplicat per 3 dóna 15. Quants CDs té?
? ·3 = 15 Resposta: 5 CDs
4) Si dividim les persones de la classe entre 3 obtenim el nombre 10. Quantes persones hi ha?
? / 3 = 10 Resposta: 30 persones
Ara, ho transformem amb equacions.
CAS 1) Suma
x + 5 = 8
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (+5) que està sumant que passa a l'altra banda restant (-5).
Solucionem l'equació:
x + 5 = 8
x = 8 - 5
x = 3
CAS 2) Resta
x - 3 = -5
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (-3) que està restant, que passa a l'altra banda sumant (+3).
Solucionem l'equació:
x - 3 = -5
x = -5 + 3
x = -2
CAS 3) Multiplicació ***
x · 3 = 15
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (3) que està multiplicant, que passa a l'altra banda dividint (/3).
Solucionem l'equació:
x · 3 = 15
x = 15 / 3
x = 5
CAS 4) Divisió
x / 3 = 10
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (/3) que està dividint, que passa a l'altra banda multiplicant (·3).
Solucionem l'equació:
x / 3 = 10
x = 10 · 3
x = 30
Equacions fàcils (suma i resta de termes)
Termes separats
Termes Barrejats
1)
Troba la solució (troba la x):
3x + 1= 5x - 3
3x - 5x = -3 - 1
-2x = -4
-2 · x = -4 (La x s'ha de quedar sola 😋)
x= -4/-2
x=+2
Comprova el resultat:
Comprovo si ho he fet bé. Poso el "+2" on hi ha la x i ha de donar el mateix a banda i banda de la igualtat.
En l'equció 3x + 1= 5x - 3, x=2 és la solució de l'equació?
3 · 2 + 1 = 5 · 2 - 3
6 + 1 = 10 - 3
7 = 7 Ho he fet bé !😃
Resol les equacions següents, fes l'autocorrecció i resol els errors en cas que en tinguis.
Troba la solució (troba la x):
2) 2x - 4 + 3x - 5 = 5x - 7 + 4x + 2
Passo els termes amb "x" a l'esquerra i els termes amb números a la dreta. Quan passo a l'altra banda, canvio de signe +/-. El signe del terme va davant.
2x - 4 + 3x - 5 = 5x - 7 + 4x + 2
2x + 3x - 5x - 4x = -7 + 2 + 4 + 5
Sumo les x i sumo els nombres.
5x - 9x = -7 + 11
-4x = + 4
-4 · x = + 4 (La x s'ha de quedar sola 😋)
x = + 4/ - 4
x = -1
Exemple 1)
Resol aquestes equacions amb parèntesi:
Quan treguis parèntesi, en les multiplicacions RECORDA:
signes iguals dóna +
signes diferents dóna -
Exemple 3 i 4) BUSCA EL MCM, troba nous numeradors i treu el denominador.
Exercics d'equacions amb solucions:
Symbolab https://es.symbolab.com/solver/linear-equation-calculator/
App mòbil per comprovar el resultat de les equacions:
PhotoMath (Android i IOS)
MalMath (Android)
REPÀS 18/12/2019
Resol i fes l'autocorrecció amb les respostes.
1) x + 1 = 3
2) x - 1 = -5
3) 2x = 16
4) x/6 = 13
5) 2x + x - 5x + 4x = 5 + 4 - 2 + 1
6) x - 1 + 4 - 2x =2x + 8 - 5x + 3
7) x=3 és resultat de l'equació següent? Fes un procediment matemàtic i escriu una frase amb la resposta:
2x + 5 = x - 4
Pista:
2·3 +5 = 3-4
6 + 5 =-1
11 =-1
11 no és igual a -1. Per tant, x=3 no és solució de l'equació.
8) 2 ·(3x+5) = 5
9) -3 (-x +2)= -9
10) -3 ·(2x-1) = -2 ·(-6x-4)
11) Repassa els problemes de fraccions de la fotocòpia i de ONMAT.
Fes el següent llistat d'equacions. Comprova el resultat aquí i posa't la nota:
https://es.symbolab.com/solver/linear-equation-calculator
Fes aquestes equacions i posa't la nota.
1) 2 · ( x + 1) = 5 R: x=3/2
2) 5x + 3 - x = 2x + 7 - x R: x=4/3
3) 4x + 3 - 5x = 3 · (x-1) R: x = 3/2
4) 4 · (x-1) + 2x = 5 - ( x - 3) R: x = 12/7
5) 2x + 3 - 5 = 5x + 4 -2x R: x= - 6
6) x + 3 · (x-1) = 6 + 2 · (x+1) R: x = 11/2
7) x + 5 = 2x + 4 - 5x R: x= -1/4
8) -2 · ( x - 1) = -3 · (x + 1 ) R: x= - 5
9) -5 · ( - x + 1 ) = -3 · (x - 1 ) R: x= 1
10) 2x - 4 · (x - 2 ) = 5x + 1 - 3 · (x+1) R: x=5/2
Repàs:
1) Fes aquestes 10 equacions. Fes l'autocorrecció. Posa't nota.
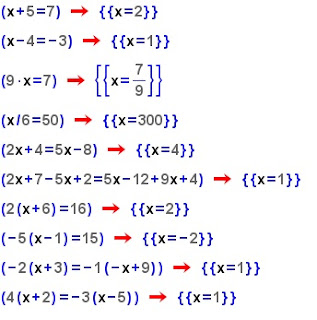
2) Comprova el resultat de l'equació 5, 6, 9 i 10.
3) Has de saber resoldre equacions per deducció.
4) Exercici de "pensar".
A primària ja feies equacions... ;-)
1) Els cotxes que té el Xavi més 5 són 8 cotxes. Quants cotxes té el Xavi?
? + 5 = 8 Resposta: 3 cotxes
2) Si a un nombre li resto 3 obtinc -5. Quin nombre és?
? - 3 = -5 Resposta: -2
3) Els CDs que té l'Íker multiplicat per 3 dóna 15. Quants CDs té?
? ·3 = 15 Resposta: 5 CDs
4) Si dividim les persones de la classe entre 3 obtenim el nombre 10. Quantes persones hi ha?
? / 3 = 10 Resposta: 30 persones
Ara, ho transformem amb equacions.
CAS 1) Suma
x + 5 = 8
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (+5) que està sumant que passa a l'altra banda restant (-5).
Solucionem l'equació:
x + 5 = 8
x = 8 - 5
x = 3
CAS 2) Resta
x - 3 = -5
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (-3) que està restant, que passa a l'altra banda sumant (+3).
Solucionem l'equació:
x - 3 = -5
x = -5 + 3
x = -2
CAS 3) Multiplicació ***
x · 3 = 15
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (3) que està multiplicant, que passa a l'altra banda dividint (/3).
Solucionem l'equació:
x · 3 = 15
x = 15 / 3
x = 5
CAS 4) Divisió
x / 3 = 10
Quant val la "x"?
La "x" s'ha de quedar sola. Fa fora el (/3) que està dividint, que passa a l'altra banda multiplicant (·3).
Solucionem l'equació:
x / 3 = 10
x = 10 · 3
x = 30
Resol les equacions següents trobant la “x” fent el procediment.
1) x + 3 = 9
|
2) x + 3=-4
|
3) x + 3=0
|
4) x +6 =-2
|
5) x - 3=-1
|
6) 2 · x = 10
|
7) (-5 )· x = 30
|
8) 2 · x = 3
|
9) x / 8 = 5
|
10) x / 20 = -5
|
Equacions fàcils (suma i resta de termes)
Termes separats
Càlcul d’equacions.
Sumem termes
Exercici 1)
3x - 2x + 6x =
8 - 7
+ 10 + 4
3x +
6x - 2x = 8 +
10 + 4 – 7
9x - 2x = 22-7
7x = 15
7 · x = 15
x= 15 / 7
Exercici 2) 5x- 8x + 9x – 2x = 5 + 9 – 4 + 1
Exercici 3) 2x – 8x + 7x – x = 4 – 6 + 9 - 3
Exercici 4) 5x – x + 9x – 2x = 5 – 8 + 9 - 1
Ves a symbolab.com. escriu l’equació I comprova si tens
bé el resultat. Pel mòbilo hi ha Photomath.
Termes Barrejats
1)
Troba la solució (troba la x):
3x + 1= 5x - 3
3x - 5x = -3 - 1
-2x = -4
-2 · x = -4 (La x s'ha de quedar sola 😋)
x= -4/-2
x=+2
Comprova el resultat:
Comprovo si ho he fet bé. Poso el "+2" on hi ha la x i ha de donar el mateix a banda i banda de la igualtat.
En l'equció 3x + 1= 5x - 3, x=2 és la solució de l'equació?
3 · 2 + 1 = 5 · 2 - 3
6 + 1 = 10 - 3
7 = 7 Ho he fet bé !😃
Resol les equacions següents, fes l'autocorrecció i resol els errors en cas que en tinguis.
Troba la solució (troba la x):
2) 2x - 4 + 3x - 5 = 5x - 7 + 4x + 2
Passo els termes amb "x" a l'esquerra i els termes amb números a la dreta. Quan passo a l'altra banda, canvio de signe +/-. El signe del terme va davant.
2x - 4 + 3x - 5 = 5x - 7 + 4x + 2
2x + 3x - 5x - 4x = -7 + 2 + 4 + 5
Sumo les x i sumo els nombres.
5x - 9x = -7 + 11
-4x = + 4
-4 · x = + 4 (La x s'ha de quedar sola 😋)
x = + 4/ - 4
x = -1
Comprova el resultat:
En l'equció 2x - 4 + 3x - 5 = 5x - 7 + 4x + 2, x=-1 és la solució de l'equació?
2 · (-+1) - 4 + 3 · (-1) - 5 = 5· (-1) - 7 + 4· (-1) + 2
-2 - 4 - 3 - 5 = -5 - 7 - 4 + 2
-14 = -16 + 2
-14 = - 14 Ho he fet bé !😃
Resol aquests 4 exemples ja resolts:En l'equció 2x - 4 + 3x - 5 = 5x - 7 + 4x + 2, x=-1 és la solució de l'equació?
2 · (-+1) - 4 + 3 · (-1) - 5 = 5· (-1) - 7 + 4· (-1) + 2
-2 - 4 - 3 - 5 = -5 - 7 - 4 + 2
-14 = -16 + 2
-14 = - 14 Ho he fet bé !😃
Exemple 1)
Exemple 2)
Exemple 3)
Equacions amb parèntesi
Equacions amb parèntesi "curtes"
Per resoldre l'equació cal OPERAR el parèntesi. Compte amb els signes!
Un nombre davant d'un parèntesi hi està MULTIPLICANT.
Exemple 1
2 · (x + 3) = 4
2·x + 2·3 = 4
2x + 6 = 4
2x = 4 - 6
2x = -2
+2·x = -2
x= -2/+2 = - 1
Exemple 2
3 · (2x - 1) = 9
3 · 2x - 3 ·1 = 9
6x - 3 = 9
6x = 9 + 3
6x = 12
+6·x = 12
x = +12/+6
x = 2
Exemple 3
-2 · (-x -3) = 10
+2x +6 = 10
2x = 10 - 6
2x = 4
2·x = 4
x = +4/+2
x = 2
Exercicis
Fes aquests exercicis i corregeix-los amb Symbolab o PhotoMath.
Exercici 1) 6 · (x + 4) = 10
Exercici 2) 2 · (3x - 4) = 15
Exercici 3) -3 · (-x -5) = 8
Exercici 4) 2 · (x + 5) = 4 · (x - 1)
Exercici 5) 5 · (2x - 1) = 3 · (x + 4)
Exercici 6) -1 · (-x -4) = -5 · (-x -3)
Equacions amb parèntesi "llargues"
Quan treguis parèntesi, en les multiplicacions RECORDA:
signes iguals dóna +
signes diferents dóna -
EQUACIONS AMB DENOMINADORS
Exemple 1 i 2) BUSCA EL MCM, troba nous numeradors i treu el denominador.
Exemple 3 i 4) BUSCA EL MCM, troba nous numeradors i treu el denominador.
Exemple 5) ES MULTIPLICA EN CREU
Exemple 6) BUSCA EL MCM, troba nous numeradors i treu el denominador.
Exercics d'equacions amb solucions:
😊 Repàs. Problemes amb solucions.
Problemes amb solució i procediment. Aquí. Fes-los a partir del problema 7.
Problemes amb solució i procediment. Aquí. Fes els problemes del "tipus" que hem fet a classe.
Pre-examen
1) La suma de 3 nombres consecutius és 222. Quins són aquests nombres? R: x= 73
2) La suma de 2 nombres consecutius és 57. Quins són aquests nombres? R: x= 28
3) La Paula té 1500 euros. En dóna una quantitat al Marc, el doble d'aquesta quantitat a la Judith i el triple del que ha donat al Marc, li dóna a l'Ethan. Quants diners dóna a cadascú? R: x= 250
4) L'Aleix té 224 sugus i en dóna una quantitat a l'Ainhoa i el triple d'aquesta quantitat al David i la Vlada. Quants en dóna a cadascú? R: x= 56
5) Si a un nombre que no saps li sumes el seu triple i li restes 25 obtens 95. Quin nombre és? R: x= 30
6) Si a un nombre que no saps li sumes la seva meitat i li sumes el seu nombre anterior, et dóna 99. Quin és aquest nombre. R: x= 40
Per preparar l'examen sobre problemes d'equacions
Sortiran: 1) Problemes de nombres 2) Problemes de repartir quantitats 3) Problemes de nombres consecutius
Has de preparar: Una "xuleta" amb 2 models de cadascun dels problemes. Fes la xuleta amb 1) l'enunciat, 2) l'equació i la resolució i 3) resposta i raonament. Títol "Xuleta de problemes d'equacions".
Inventa't 2 problemes de cada tipus. Escriu 1) l'enunciat, 2) l'equació i la resolució i 3) resposta i raonament. Títol "Problemes inventats". És molt important que raonis i comprovis el resultat.
Prepararem l'examen en parelles. Indica si ets professor o alumne i el nom del teu professor o alumne.
PROBLEMES D'EQUACIONS DE GEOMETRIA. Tipus 1
Inventa't l'enunciat per a cadascuna d'aquestes equacions.
Exemple:
Problema 1)
1. Equació:
x + x + x + x = 40
2. Resolem l'equació:
4x = 40
4 · x = 40
x= 40/4
x =10 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un quadrat mesura 40 cm. Quant mesura cada costat?
Problema 2)
1. Equació:
x + x + x = 45
2. Resolem l'equació:
3x = 45
3 · x = 45
x= 45/3
x =15 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un triangle equilàter mesura 45 cm. Quant mesura cada costat?
4. Escric la resposta del problema amb una frase i unitats.
** Exercicis. Ara, que cadascú del grup s'inventi 1 problema de cada i els resoleu amb els 4 passos proposats.
Problema 3)
1. Equació:
x + 2x + x + 2x = 60
2. Resolem l'equació:
6x = 60
6 · x = 60
x= 60/6
x =10 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un rectangle mesura 60 cm. Si el costat llarg és el doble que el costat curt, quant mesura cada costat? Situa a la figura el costat que val x i el costat que val 2x.
x és la solució del costat curt. (10 cm)
2x és la solució del costat llarg. (10 · 2 = 20 cm)
4. Escric la resposta del problema amb una frase i unitats.
Problema 4)
1. Equació:
x + 2x + 2x = 100
2. Resolem l'equació:
5x = 100
5 · x = 100
x= 100/5
x =20 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un triangle isòsceles (2 costat iguals i un de diferent) mesura 100 cm. Si els costats llargs són el doble que el costat curt, quant mesura cada costat? Situa a la figura el costat que val x i el costat que val 2x.
x és la solució del costat curt. (20 cm)
2x és la solució del costat llarg. (20 · 2 = 40 cm)
4. Escric la resposta del problema amb una frase i unitats.
1. Equació:
x + x + x = 45
2. Resolem l'equació:
3x = 45
3 · x = 45
x= 45/3
x =15 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un triangle equilàter mesura 45 cm. Quant mesura cada costat?
** Exercicis. Ara, que cadascú del grup s'inventi 1 problema de cada i els resoleu amb els 4 passos proposats.
Problema 3)
1. Equació:
x + 2x + x + 2x = 60
2. Resolem l'equació:
6x = 60
6 · x = 60
x= 60/6
x =10 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un rectangle mesura 60 cm. Si el costat llarg és el doble que el costat curt, quant mesura cada costat? Situa a la figura el costat que val x i el costat que val 2x.
x és la solució del costat curt. (10 cm)
2x és la solució del costat llarg. (10 · 2 = 20 cm)
Problema 4)
1. Equació:
x + 2x + 2x = 100
2. Resolem l'equació:
5x = 100
5 · x = 100
x= 100/5
x =20 és la solucíó.
3. Escric l'enunciat d'un problema on puc aplicar aquesta equació. Dibuixo la figura geomètrica i indico que els costats valen "x".
El perímetre d'un triangle isòsceles (2 costat iguals i un de diferent) mesura 100 cm. Si els costats llargs són el doble que el costat curt, quant mesura cada costat? Situa a la figura el costat que val x i el costat que val 2x.
x és la solució del costat curt. (20 cm)
2x és la solució del costat llarg. (20 · 2 = 40 cm)
4. Escric la resposta del problema amb una frase i unitats.
Problema 5)
Fes els 4 passos amb la informació que se't dóna.
1. Equació:
x + x+1 + x+2 = 33
" El perímetre d'un triangle escalè (3 costats diferents) mesura 33 cm. Quant valen els 3 costats diferents d'un triangle escalè, sabent que el costat mitjà és 1 cm major que el petit, i el costat gran és 2 cm major que el costat petit".
Indica al dibuix el costat petit (x) el costat mitjà (x+1) i el costat gran (x+2)
** Ara que ja ets un expert, inventat't i resol 1 problema de cada tipus. Escriu l'enunciat, la figura geomètrica amb les "x" i l'equació. Resol el problema i escriu el resultat amb una frase i unitats.
Passos: 1) Equació 2) Dibuix de la figura amb les "x" i dades 3) Resolem l'equació 4) Resposta amb una frase.
MODEL. NO ES COPIA.
1) Quant mesuren els costat d'un quadrat de 2 cm de perímetre?
1) x+x +x +x=2
2)
3) x+x +x +x=2
4x =2
x=2/4
x=0,5 cm
4) Cada costat del quadrat mesura 0,5 cm.
1) Quant mesuren els costats d'un quadrat de perímetre 320 cm? R: 80 cm.
2) Quant mesuren els costat d'un triangle equilàter de perímetre 24 cm? R: 8 cm.
3) El costat llarg d'un rectangle mesura el triple que el curt. Quant mesura cada costat si el perímetre val 160 m? R:20 curt. R:60 llarg.
4) En un triangle isòsceles (2 costats iguals i 1 de diferent), els dos costats llargs fan el quàdruple (multiplicat per 4 ;-)) que el costat curt. Si el perímetre mesura 90 cm, quant mesuren els costats? R: 10 cm curt. 40 cm els llargs.
5) En un triangle escalè (tots els costats diferents), el costat mitjà mesura 5 cm més que el costat curt. El costat gran mesura 10 cm més que el costat curt. Si el perímetre és 75 cm, quant mesura cada costat? R: Equació: x+ x+5 + x+10 = 75. Costats: 20 cm, 25 cm, 30 cm.
6) Inventa't un problema similar amb un pentàgon o hexàgon. (si et sobra temps)
CORRECCIÓ
1) Quant mesuren els costats d'un quadrat de perímetre 320 cm? R: 80 cm.
x + x + x + x = 320
4x=320
4·x=320
x=320/4
x=80 cm
R: Cada costat fa 80 cm. La resposta és coherent perquè 80 x 4 dóna 320 cm.
2) Quant mesuren els costat d'un triangle equilàter de perímetre 24 cm? R: 8 cm.
x + x + x = 24
3x=24
3·x=24
x=24/3
x=8 cm
R. Cada costat fa 8 cm. La resposta és coherent perquè 8 x 3 dóna 24 cm.
3) El costat llarg d'un rectangle mesura el triple que el curt. Quant mesura cada costat si el perímetre val 160 m? R:20 curt. R:60 llarg.
3x + 3x + x + x = 160
8x=160
8·x=160
x=160/8
x=20 cm
R. El costat curt mesura 20 cm i el llarg 60 cm. Costa. La resposta és coherent perquè si sumes tots els costats dóna 60 + 60 + 20 + 20 = 160 cm.
4) En un triangle isòsceles (2 costats iguals i 1 de diferent), els dos costats llargs fan el quàdruple (multiplicat per 4 ;-)) que el costat curt. Si el perímetre mesura 90 cm, quant mesuren els costats? R: 10 cm curt. 40 cm els llargs.
x + 4x + 4x = 90
9x=90
9·x=90
x = 90/9
x=10 cm
R. Costat curt 10 cm. Costat llarg 40 cm.. La resposta és coherent perquè si sumes els costats (10 + 40 + 40) dóna 90.
5) En un triangle escalè (tots els costats diferents), el costat mitjà mesura 5 cm més que el costat curt. El costat gran mesura 10 cm més que el costat curt. Si el perímetre és 75 cm, quant mesura cada costat? R: Equació: x+ x+5 + x+10 = 75. Costats: 20 cm, 25 cm, 30 cm.
x + x+5 + x+10 = 75
3x + 15 =75
3x =75 - 15
3x = 60
3·x = 60
x=60/3
x=20 cm
R. El costat curt fa 20 cm, el mitjà 25 cm i el llarg 30 cm.. La resposta és coherent perquè si sumes els costats (20 + 25 + 30) dóna 75 cm.
6) Inventa't un problema similar amb un pentàgon o hexàgon. (si et sobra temps)
PROBLEMES DE NOMBRES. Tipus 2
Fes correspondre cada enunciat amb la seva equació. Després resol el problema amb els 4 passos.
Enunciats:
1. Si multipliques un nombre que no saps per 5 i li restes 40 obtens 25. Quin és aquest nombre? (El nombre és la "x").
2. Si a un nombre natural (x) li sumes l'anterior (x-1) i després li sumes el nombre següent (x+1), obtens 111. Quin és el nombre natural?
3. Si a un nombre (x) li sumes la tercera part (x/3) i després li sumes 5, obtens 21. Quin és aquest nombre (x)?
4. Si a 15 li restem el doble d'un nombre que no conec (2x), obtinc 1. Quin és aquest nombre?
Equacions:
A. 15 - 2x = 1 Solució : x= 7
B. x + x/3 + 5 = 21 Solució : x= 12
C. x + (x-1) + (x+1) = 111 Solució : x= 37
D. 5x - 40 = 25 Solució : x= 13
Solucionari:
1. Si multipliques un nombre que no saps per 5 i li restes 40 obtens 25. Quin és aquest nombre? (El nombre és la "x").
D. 5x - 40 = 25 Solució : x= 13
2. Si a un nombre natural (x) li sumes l'anterior (x-1) i després li sumes el nombre següent (x+1), obtens 111. Quin és el nombre natural?
C. x + (x-1) + (x+1) = 111 Solució : x= 37
3. Si a un nombre (x) li sumes la tercera part (x/3) i després li sumes 5, obtens 21. Quin és aquest nombre (x)?
B. x + x/3 + 5 = 21 Solució : x= 12
4. Si a 15 li restem el doble d'un nombre que no conec (2x), obtinc 1. Quin és aquest nombre?
A. 15 - 2x = 1 Solució : x= 7
PROBLEMES DE REPARTIR QUANTITATS. Tipus 3
Exemple 1
1) Equació: x + 2x +3x = 240
2) Resolem l'equació:
x + 2x +3x = 240
6x = 240
x = 240/6
x = 40
3) Enunciat. El Pau té 240 € i en dona una quantitat a l'Aleix. Dóna el doble d'aquesta quantitat a la Maria i el triple d'aquesta quantitat al Pere. Quants diners dona a cadascú?
4) Resposta i reflexió del resultat. Aleix 40 €, Maria 80 € i Pere120 €. És correcta perquè si sumes aquestes quantitats dóna 240 €.
Exemple 2
1) Equació: x + 3x +2 · 3x = 500
x + 3x +6x = 500
2) Resolem l'equació:
x + 3x +6x = 500
10x = 500
x = 500/10
x = 50
3) Enunciat. Reparteixes 500 € i en dones una quantitat a la Paula, el triple del que dones a la Paula ho dones a l'Eric i el doble del que dones a l'Eric ho dones a la Judith (2 · 3x). Quant tindrà cadascú?
4) Resposta i reflexió del resultat. Paula 50€. Eric 150€. Judith 300€. Tot sumat dóna 500 €.
Exemple 3
1) Equació: x + x+ 50 + x + 500 = 670
2) Resolem l'equació:
x + x+ 50 + x + 500 = 670
3x + 550 = 670
3x = 670 - 550
3x = 120
x = 120 / 3
x= 40
3) Enunciat. El Manel té uns diners que no sabem. El Pol té els diners del Manel més 50 €. L'Emma té els diners del Manel més 500 €. Si en total tenen 670 euros, quants diners té cadascú?
4) Resposta i reflexió del resultat. Manel 40 €. Pol 90 €. Emma 540 €. Tot sumat dóna 670 €.
PROBLEMES DE NOMBRES CONSECUTIUS. Tipus 4
Exemple 1
1) Equació: x + x + 1 + x + 2 = 63
2) Resolem l'equació:
x + x + 1 + x + 2 = 63
3x + 3 = 63
3x = 63 - 3
3x= 60
x = 60/3
x = 20
3) Enunciat. La suma de 3 nombres consecutius dóna 63. Quins són aquests nombres?
4) Resposta i reflexió del resultat. Són 20, 21 i 22 perquè sumats donen 63.
Exemple 2
1) Equació: x + x + 1 = 251
2) Resolem l'equació:
x + x + 1 = 251
2x + 1 = 251
2x = 251 - 1
2x = 250
x = 250/2
x = 125
3) Enunciat. La suma de 2 nombres consecutius dóna 251. Quins són aquests nombres?
4) Resposta i reflexió del resultat. Són 125 i 126 perquè sumats donen 251.
Ara ho faig jo:
Inventa't 4 problemes de nombres consecutius. Escriu: 1) Enunciat 2) Equació i resolució de l'equació 3) Resultat i reflexió sobre el resultat.
Resultats de l'examen per fer la correcció:
1) 3 euros i 8 euros. 2) 23 euros. 3) 9,9 euros 4) t= (c-3)/0,05 5) 580 minuts
6) 9,6 hores / 9 hores 39 minuts 7) 1r gràfic 8) 540 $ i 860 $ 9) 620 $ 10) V= (M+180)/8
11) 109,43 mph 12) 32 F i 86 F 13) 77 F 14) C= (5F-160) / 9 15) 10 ºC
16) Laia ªF i Jordi ºC 17) 56,07 euros 18) 69 $ 19) opció b)
CÀLCUL AMB FÓRMULES
Exercici 1)
- 1) Funció 1. c = 3 + 0,5 · t (cost = 3 + 0,5 · temps) cost en euros i temps en minuts
a. Quant pagues al mes si truques 100 minuts? I 2 hores?
b. Escriu la funció temps en funció del cost.
c. Quant temps en minuts has trucat si pagues 50 euros?
d. Passa els minuts a hores (1 hora = 60 minuts)
- 2) Funció 2. c = 5+ 0,02 · t (cost = 5 + 0,02 · temps) cost en euros i temps en minuts
a. Quant pagues al mes si truques 60 minuts? I 3 hores?
b. Escriu la funció temps en funció del cost.
c. Quant temps en minuts has trucat si pagues 60 euros?
d. Passa els minuts a hores (1 hora = 60 minuts)
- 3) Funció 3. c = 7 + 0,10 · t (cost = 7 + 0,10 · temps) cost en euros i temps en minuts
a. Quant pagues al mes si truques 150 minuts? I 5 hores?
b. Escriu la funció temps en funció del cost.
c. Quant temps en minuts has trucat si pagues 30 euros?
d. Passa els minuts a hores (1 hora = 60 minuts)
Correcció
Exercici 2)Correcció
2.1) Funció 1. M = 7V - 170 (Multa= 7· Velocitat - 170) multa en dòlars i velocitat en milles per hora (mph)
1 1 milla equival a 1,6 km
a a. 1 mph = ....... km/h ; 5 mph = ....... km/h
b b. Si vas a una velocitat superior a 60 mph, et posen una multa. Quant hauràs de pagar de multa, si vas a 70 mph? Aplica la fórmula M= 7V - 170.
c c. Escriu la funció velocitat en funció de la multa. V= ................
d d. Si pagues 390 dòlars de multa, a quina velocitat anaves?
1 1 milla equival a 1,6 km
a a. 1 mph = ....... km/h ; 25 mph = ....... km/h
b b. Si vas a una velocitat superior a 70 mph, et posen una multa. Quant hauràs de pagar de multa, si vas a 80 mph? Aplica la fórmula M= 8V - 180.
c c. Escriu la funció velocitat en funció de la multa. V= ................
d d. Si pagues 500 dòlars de multa, a quina velocitat anaves?
REPRESENTACIÓ GRÀFICA
Tutorial. Com fer gràfics a partir d'una taula de dades amb Excel. Aquí.
Fooplot
http://fooplot.com/?lang=es#W3sidHlwZSI6MCwiZXEiOiJ4XjIiLCJjb2xvciI6IiMwMDAwMDAifSx7InR5cGUiOjEwMDB9XQ--
Grapher
Descarrega't al mòbil el programa Grapher (Per Android)
https://play.google.com/store/apps/details?id=com.opticron.grapher
Quick Graph
Descarrega't al mòbil el programa Quick Graph (Per iPhone)
https://itunes.apple.com/es/app/quick-graph-tu-calculadora/id292412367?mt=8
FUNCIONS. Taula i gràfic.
😊😊Repàs per a l'examen de funcions.
1) Has de tenir fet el dossier "Funcions" amb tots els exercicis acabats i corregits.
2) Fes aquestes funcions de repàs:
2.1) Representa les funcions següents. Fes la taula primer i després del gràfic.
Taula: Indica: x, y, punt.
Gràfic. Fes el sistema de coordenades amb els 4 quadrants i indica: l'eix de les x, l'eix de les y i els valors positius i negatius.
2.2) Funcions per practicar:
y = 2+0,5·x
Corregeix-te els resultats amb el programa Grapher o QuickGraph.
2) Representa les funcions següents:
FUNCIONS que es representen amb una paràbola
FUNCIONS que es representen amb una recta
3) Escriu al costat de la línia, quina és la funció de cada gràfic.
Funció tipus y= ax
1) y= x
2 )y=2x
3) y=3x
4) y= 0.5x
5) y= 0.25x
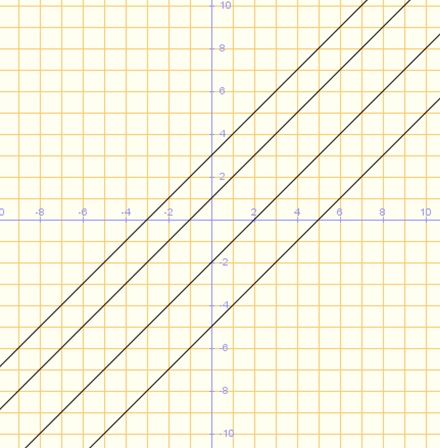
Escriu al costat de la línia, quina és la funció de cada gràfic.
Funció tipus y= x + a y= x - a
1) y= x +1
2) y= x+3
3) y= x-2
4) y= x-5
Tutorial. Com fer gràfics a partir d'una taula de dades amb Excel. Aquí.
Fooplot
http://fooplot.com/?lang=es#W3sidHlwZSI6MCwiZXEiOiJ4XjIiLCJjb2xvciI6IiMwMDAwMDAifSx7InR5cGUiOjEwMDB9XQ--
Grapher
Descarrega't al mòbil el programa Grapher (Per Android)
https://play.google.com/store/apps/details?id=com.opticron.grapher
Quick Graph
Descarrega't al mòbil el programa Quick Graph (Per iPhone)
https://itunes.apple.com/es/app/quick-graph-tu-calculadora/id292412367?mt=8
FUNCIONS. Taula i gràfic.
😊😊Repàs per a l'examen de funcions.
1) Has de tenir fet el dossier "Funcions" amb tots els exercicis acabats i corregits.
2) Fes aquestes funcions de repàs:
2.1) Representa les funcions següents. Fes la taula primer i després del gràfic.
Taula: Indica: x, y, punt.
Gràfic. Fes el sistema de coordenades amb els 4 quadrants i indica: l'eix de les x, l'eix de les y i els valors positius i negatius.
2.2) Funcions per practicar:
y = 3x
y = x+3
y = 3x2
y = -2x2
y = 2+0,5·x
Corregeix-te els resultats amb el programa Grapher o QuickGraph.
2) Representa les funcions següents:
FUNCIONS que es representen amb una paràbola
Funció 1) y = x2
1) Taula:
x
|
-5
|
-2
|
-1
|
0
|
+1
|
+2
|
+5
|
y=x2
|
y=(-5)2 =(-5)·(-5)= +25
|
y=(+1)2 = +1
| |||||
punt (x, y)
|
(-5, +25)
|
(+1, +1)
|
2) Gràfic:
Funció 2) y = x2
1) Taula:
x
|
-5
|
-2
|
-1
|
0
|
+1
|
+2
|
+5
|
y= x2
|
y=(-5)2 +3= +25+3=+28
|
y=(+1)2 +3= +1+3=+4
| |||||
punt (x, y)
|
(-5, +28)
|
(+1, +4)
|
2) Gràfic:
Funció 3) y = x2
1) Taula:
x
|
-5
|
-2
|
-1
|
0
|
+1
|
+2
|
+5
|
y= x2
| |||||||
punt (x, y)
|
2) Gràfic:
FUNCIONS que es representen amb una recta
3) Escriu al costat de la línia, quina és la funció de cada gràfic.
Funció tipus y= ax
1) y= x
2 )y=2x
3) y=3x
4) y= 0.5x
5) y= 0.25x
Escriu al costat de la línia, quina és la funció de cada gràfic.
Funció tipus y= x + a y= x - a
1) y= x +1
2) y= x+3
3) y= x-2
4) y= x-5
