Dau virtual. Aquí.
Projectes de Matemàtiques del curs. Aquí.
Vídeos dels temes que farem. Aquí.
Exercicis de repàs de Matemàtiques 1r d'ESO amb solucions:
Exercics del curs amb solucions:
Primer trimestre
Índex
Tema 1. Nombres naturals (i enters)
Tema 2. Nombres enters. Càlcul i problemes
Tema 3. Potències i arrels
Tema 4. M.C.M. Fraccions
Índex
Tema 1. Nombres naturals (i enters)
Tema 2. Nombres enters. Càlcul i problemes
Tema 3. Potències i arrels
Tema 4. M.C.M. Fraccions
Tema 5. Proporcionalitat i percentatges
---------------------------------
Tema 1. NOMBRES NATURALS (i ENTERS)
---------------------------------
Tema 1. NOMBRES NATURALS (i ENTERS)
Exercicis del tema amb solucions:
Jocs matemàtics
Nombres naturals: 1, 2, 3, 4, ...
Nombres enters: ..., -4, -3, -2, -1, 0, +1, +2, +3, +4, ...
Jerarquia de les operacions:
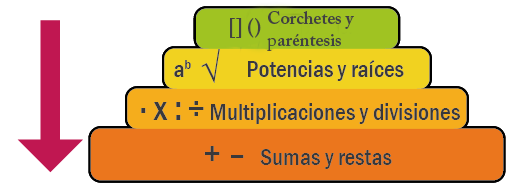
Exemple 2:
+ 42 : 8 - 62 : 12 + 2 - 2 ·3 + 60: 15 + 1 =
1) APUNTS. Prioritat d'operacions. Criteri de signes
Font: https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjs9Qn62UhFkVklKa9VX5HL5Gdlamh07Tavd4Oe27vrN3KsWRfn55oVp_i2OeuK0ERPy6hGS_XZDNHNXhCDonUECe8zHT1_6yghQAYCgAGFP-JkAXcf2ZSTz0NQhKA-czt2NqQYKFQFs18/s1600/raices+cuadradas+del+1+al+20.png
Font: http://www.bartolomecossio.com/MATEMATICAS/cuadrados_y_cubos.html
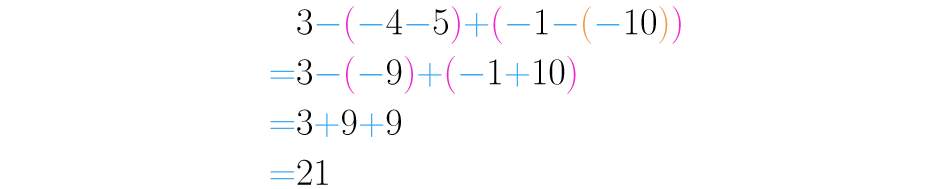
Valor absolut i oposat d'un nombre
a) 2 · (5 + 6) =
Truquito "Tinc -dec"
4 casos de "tinc-dec"
+ 2+ 7 = + 9
tinc tinc = tinc
- 2 - 7 = - 9
dec dec = dec
+2 - 7 = - 5
tinc dec = resta el gran menys el petit i guanya el signe la xifra més gran (-)
- 2 + 7 = + 5
dec tinc= resta el gran menys el petit i guanya el signe la xifra més gran (+)
Practica:
1) + 5 - 9 =
2) - 4 -3 =
3) + 3 + 1 =
4) - 10 + 6 =
5) + 25 - 5 =
6) + 3 - 4 =
7) + 5 - 5 =
8) + 4 - 9 =
9) - 7 - 5 =
10) + 5 + 8 =
Cas 1: Sumes i restes
No ho faig directament . Agrupo els que sumen junts i els que resten junts.
Exemple 1:
+ 3 - 5 + 9 - 10 + 4 =
+ 3 - 5 + 9 - 10 + 4 = (marco els que sumen i els que resten)
+ 3 + 9 + 4 - 5 - 10 = (agrupem els que sumen i els que resten)
+ 16 - 15 = + 1
tinc dec
Exemple 2:
- 6 + 8 - 7 + 0 - 4 + 1 =
..
Exemple 3:
-5 + 7 - 9 + 4 - 3 =
...
Cas 2 : Suma, resta, multiplicació i divisió
Exemple 1:
+ 3 · 4 - 10 : 2 + 8 - 6 : 3 =
+ 3 · 4 - 10 : 2 + 8 - 6 : 3 = ( resolc primer les multiplicacions i divisons en ordre)
+ 12 - 5 + 8 - 2 =
+12 + 8 - 5 - 2 = (agrupem els que sumen i els que resten)
+ 20 - 7 = + 13
tinc dec
Exemple 2:
- 50 : 25 + 3 · 5 - 24 : 6 + 2 - 1 + 15 : 15 =
Cas 3: Suma, resta, multiplicació i divisió, potències i arrels
Exemple 1:
+ 23 : 4 - 102 : 25 + 8 - 5: 5 + 40 : 8 + 5 · 2 =
+ 23 : 4 - 102 : 25 + 8 - 5: 5 + 40 : 8 + 5 · 2 =
+ 8 : 4 - 100 : 25 + 8 - 5: 5 + 40 : 8 + 5 · 2 =
+ 2 - 4 + 8 - 1 + 5 + 10 =
+ 2 + 8 + 5 + 10 - 4 - 1 =
+ 25 - 5 = + 20
Exemple 2:
+ 42 : 8 - 62 : 12 + 2 - 2 ·3 + 60: 15 + 1 =
Exemple 3:
-102 + 25 - 30 : 6 + 2 · 3 - 100 - 40 : 8 + 3 · 5 =
25 - 30 : 6 + 2 · 3 - Cas 4: Suma, resta, multiplicació i divisió, potències i arrels, parèntesi i corchetes
Exemple 1.
2 - 3 · [ - 2 + 10 - 4 · ( - 1 + 3 : 3) - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 4 · ( - 1 + 3 : 3) - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 4 · ( - 1 + 3 : 3) - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 4 · ( - 1 + 1 ) - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 4 · 0 - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 0 - 8 ] - 2 =
2 - 3 · 0 - 2 =
2 - 0 - 2 =
+ 2 - 2 = 0
Exemple 2.
3 + [5 · 6 + 4 · ( 12 : 4 + 5 · 2 ) + 24 : 3 ] =
Solució: 93
Exemple 3.
[ 8 : 2 + 6 · ( 2 + 1 ) ] - [10 : 2 + 15 : ( 1 +2 ) ] =
Solució:12
2 - 3 · [ - 2 + 10 - 4 · ( - 1 + 1 ) - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 4 · 0 - 8 ] - 2 =
2 - 3 · [ - 2 + 10 - 0 - 8 ] - 2 =
2 - 3 · 0 - 2 =
2 - 0 - 2 =
+ 2 - 2 = 0
Exemple 2.
3 + [5 · 6 + 4 · ( 12 : 4 + 5 · 2 ) + 24 : 3 ] =
Solució: 93
Exemple 3.
[ 8 : 2 + 6 · ( 2 + 1 ) ] - [10 : 2 + 15 : ( 1 +2 ) ] =
Solució:12
Practica tot el que saps ;-):
Tema 2. NOMBRES ENTERS
Exercicis del tema amb solucions:
Jocs matemàtics
MalMath
Descarrega't al mòbil el programa MalMath (Android)
Nombres natural: 1, 2, 3, 4, ...
Nombres enters: ..., -4, -3, -2, -1, 0, +1, +2, +3, +4, ...
Prioritat de les operacions
Truquito "Tinc-dec"
Regla dels signes amb nombres enters (escut)
Quant tenim multiplicacions, divisions o hem de treure parèntesi fem:
Signes iguals +
Signes diferents -
Multiplicació
(+6) · (+3) = + 18
(-6) · (-3) = + 18
(+6) · (-3) = - 18
(-6) · (+3) = - 18
Divisió
(+6) : (+3) = + 2
(-6) : (-3) = + 2
(+6) : (-3) = - 2
(-6) : (+3) = - 2
Treure "escut" o parèntesi
+ (+6) = +6
- (-6) = +6
+(-6) = - 6
- (+6) = - 6
Compte no confondre-ho amb suma i resta "Tinc-dec".
1.1) Operació final SUMA I RESTA tinc-dec. 4 CASOS:
+ 3 + 5 = + 8
tinc tinc = tinc
- 3 - 5 = - 8
dec dec = dec
+3 - 5 = - 2
tinc dec = resta el gran menys el petit i guanya el signe la xifra més gran (-5)
- 3 + 5 = + 2
dec tinc= resta el gran menys el petit i guanya el signe la xifra més gran (+5)
1.2) Criteri per treure parèntesi, multiplicació, divisió.
signes iguals ................... + (més)
Exemple:
-(-5) = +5
+ (+3) = +3
(-6) · (-2) = +12
(+60) : (+30) = +2
signes diferents ............... - (menys)
Exemple :
-(+2) = -2
- (+7) = -7
(+7) · (-6) = -42
(-30) : (+10) = -3
1.3) Recorda!!!
** La divisió i multiplicació de 2 nombres amb "escut" donen un altre nombre amb "escut = parèntesi". Ex: (+12): (-4) = (-3)
** 2 signes no poden anar seguits, han d'estat separats per un parèntesi. Ex: + - 6 = + (-6)
** Operació final: tinc -dec.
Ex: - 9 + 5 = - 4
dec tinc dec
2) Càlcul amb nombres enters
Cas 1. Suma i resta de nombres enters
Exemple 1:
(-3) + (+9) - (-2) + 0 - (-1) =
+ (-3) + (+9) - (-2) + 0 - (-1) =
+ (-3) + (+9) - (-2) + 0 - (-1) =
-3 +9 +2 +0 +1 = (trec l' "escut")
+9 +2 +0 +1 -3 =
+12 -3 = +9
Exemple 2:
(-6) + (+7) - ( +1) + (-5) =
+ (-6) + (+7) - ( +1) + (-5) =
+ (-6) + (+7) - ( +1) + (-5) =
...
Cas 2. Suma i resta, multiplicació i divisió de nombres enters
Recorda: ** La divisió i multiplicació de 2 nombres amb "escut" donen un altre nombre amb "escut". Ex: (+12): (-4) = (-3)
Exemple 1:
(-6) : (+2) + (-100) : ( +20) + 1 - (-2) · 3 + (-1) =
(-6) : (+2) + (-100) : ( +20) + 1 - (-2) · 3 + (-1) =
+ (-3) + (-5) +1 - (-6) + (-1) = (fillet amb "escut")
-3 -5 +1 + 6 -1 = (trec "escut")
+1 +6 -3 -5 -1 =
+7 -9 = - 2
Exemple 2:
9 + (+8) · 2 + (-7) - (-30) : (+5) - (-50) : ( +25) =
9 + (+8) · 2 + (-7) - (-30) : (+5) - (-50) : ( +25) =
...
Cas 3. Suma i resta, multiplicació i divisió, potències i arrels de nombres enters
Recorda:
Quadrats i arrels quadrades:
Font: https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjs9Qn62UhFkVklKa9VX5HL5Gdlamh07Tavd4Oe27vrN3KsWRfn55oVp_i2OeuK0ERPy6hGS_XZDNHNXhCDonUECe8zHT1_6yghQAYCgAGFP-JkAXcf2ZSTz0NQhKA-czt2NqQYKFQFs18/s1600/raices+cuadradas+del+1+al+20.png
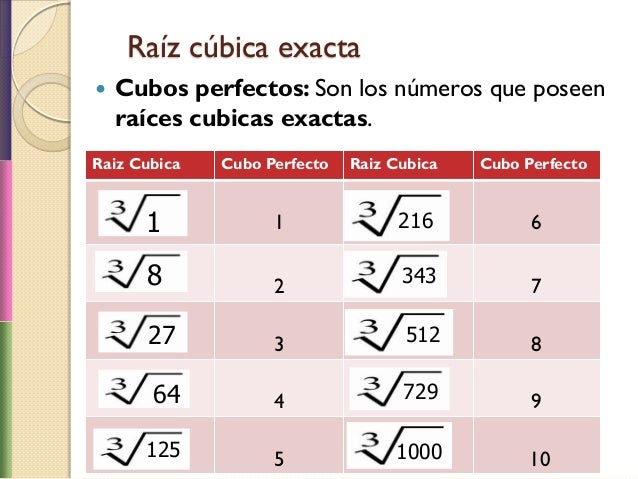
Cubs i arrels cúbiques:
Quadrats i cubs... i geometria:
Font: http://www.bartolomecossio.com/MATEMATICAS/cuadrados_y_cubos.html
Font: http://www.bartolomecossio.com/MATEMATICAS/cuadrados_y_cubos.html
Potències amb nombres enters:
Per què 50 = 1?
Exemple 1:
Exemple 2:
Cas 4. Suma i resta, multiplicació i divisió, potències i arrels, parèntesi i corchetes de nombres enters
Exemple 1:
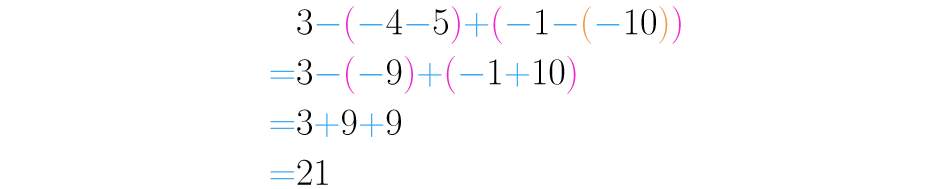
Exemple 2:
(1 - 7) : ( 2 - 4) + (12 - 10 ) : (1 - 2 ) =
Exemple 3:
4 - 6 : (6 - 4 ) - [16 : (9 - 1) - 3 ] =
Exemple 4, 5, 6 i 7:
Valor absolut i oposat d'un nombre
Propietat distributiva. Calcula la 2 maneres
a) 2 · (5 + 6) =
1a manera 2 · (5 + 6) = 2 · (+11) = + 22
2a manera 2 · 5 + 2 · 6 = 10 + 12 = + 22 Apliquem la propietat distributiva
b) 3 · (4 + 2) =
1a manera 3 · (4 + 2) = 3 · (+6) = + 182a manera 3 · 4 + 3 · 2 = 12 + 6 = + 18 Apliquem la propietat distributiva
c) -7 · (9 - 4) =
1a manera -7 · (9 - 4) = (-7) · (+5) = - 352a manera -7 · 9 - (-7) · 4 = - 63- (-28) = - 63 + 28= - 35 Apliquem la propietat distributiva
d) -2 · (5 - 6) =
1a manera -2 · (5 - 6) = (-2) · (-1) = +22a manera -2 · 5 - (-2) · 6 = - 10- (-12) = - 10 + 22= -+2 Apliquem la propietat distributiva
Altres exemples per practicar:
Correcció:
Repàs operacions amb enters per a l'examen
Resol indicant el procediment:1) + 5 - 3 + 4 - 8 + 2 =2) - 9 + 3 - 8 + 5 - 0 =3) -(-2) + (+9) - (+4) - (-10) =4) 5 - (-2 + 3 ) - (4 - 6 ) + (-3 ) =5) 5 · 3 - 4 · 22 - 8 =6) (-2) · (+5 ) - (-20) : (+5) + 3 =7) (-3) · (+2) - (+20) : (-4) =
8) Fes les operacions combinades següents. Corregeix cada exercici després de fer-lo i no passis al següent fins que no el tinguis entès i correcte. IMPORTANT! ;-)
Correcció:
Operacions combinades difícils:
PROBLEMES DE NOMBRES ENTERS
Copia l'enunciat. Dibuixa la la recta numèrica. Resol del problema. Fes l'autocorrecció:
Problemes de nombres enters. Sense solució. Amb solució.
Pre-examen:
1) + 5 - 6 + 9 - 4 =
2) - ( - 3 ) - 2 + ( -8 ) - (-2) + 0 - 4 =
3) 4 · 8 - 5 · (-2) + (-18) : (+6) =
4) Aquí hi aniria les operacions difícils tipus exercici 44, 45 ;-)
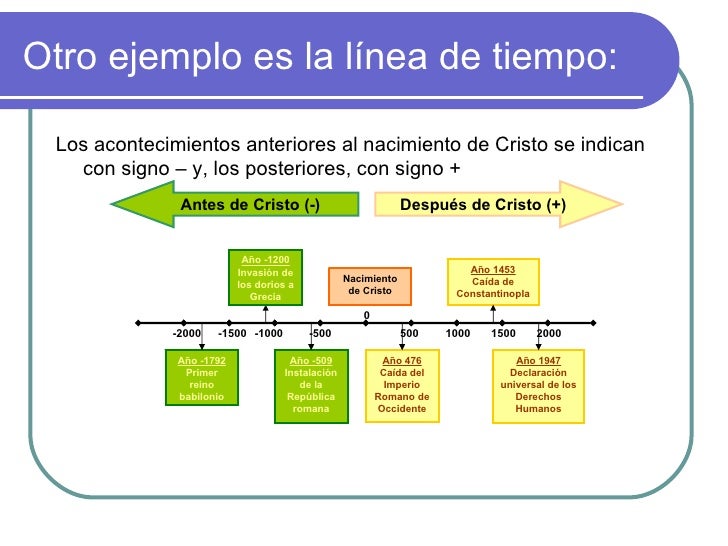
5) Un romà va néixer l'any 12 a.C. i va morir el 25 d.C. Quants anys va viure? (Línia del temps, procediment EN HORITZONTAL, i resposta amb una frase. Càlculs en un "costadet")
6) Una romà va néixer l'any 15 a.C. i va viure 32 anys. A quin any va morir?
7) Estic a la planta -5 d'un edifici, pujo 8 plantes i en baixo 3. A quina planta estic al final?
8) La mostra d'un experiment està a -17ºC i la temperatura puja 26ºC. Quina és la temperatura final?
9) Inventa't un problema on hi surtin nombres positius i negatius: enunciat, resolució, resposta amb una frase.
Tema 3. Potències i arrels
Exercicis del tema amb solucions:
Jocs matemàtics
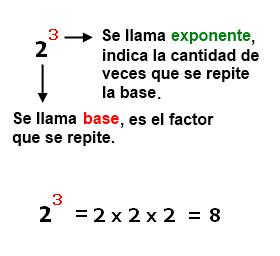
Normes de les potències:
Font: https://sites.google.com/site/algebra2611/unidad-2/leyes-de-los-exponentes-y-radicales
Tema 4. M.C.M. Fraccions
Exercicis del tema amb solucions:
Respostes al full de repàs de 17/11. Autocorregeix-te els exercicis i refes el que sigui incorrecte. Posa't la nota: (.... bé / 11) · 10 = ........
1. Tardarà 180 dies.
2. a) 80 € b) 20 € c) 225 € d) 42 € .
3. 1) 29/15 2) -39/20 3) 103/60 4) 2/15 5) -55/27 6) 47/20
4. Ana 90 cromos. Núria 30 cromos. Andoni 120 cromos.
5. La M.Loli té 50 sugus. Sobren 75 sugus. A la bossa al principi hi havia 125 sugus.
6. Martí 45 papers. Anna 30 papers. Ona 15 papers. L'Ona recull 1/6.
Tema 4.1 Mínim comú múltiple (M.C.M)
Joc matemàtic
Problemes
Problema 1) La Judith mira el mòbil cada 8 minuts i el Gerard cada 6 minuts. Si ara acaben de mirar el mòbil, en quin minut tornaran a coincidir?
Primera manera) MCM pel mètode dels múltiples
Múltiples de 8: M (8) = {0, 8, 16, 24, 32, ...}
Múltiples de 6: M (6) = {0, 6, 12, 18, 24, 30, ...}
El primer número que coincideix és el múltiple comú més petit que és el mínim comú múltiple (mcm) que és el 24.
Resposta: Tornaran a mirar el mòbil al minut 24.
Segona manera) MCM pel mètode de les potències
Recorda els números primers: 2, 3, 5, 7, 11, 13...
Recorda també els criteris de divisibilitat:
8 2 6 2
4 2 3 3
2 2 1)
1)
8= 23 6= 2 · 3
Per calcular l'mcm de 8 i 6, múltiplico els número "diferents" que tene la potència major.
m.c.m. (8, 6) = 23· 3 = 8 · 3 = 24
Resposta: Tornaran a mirar el mòbil al minut 24.
Recorda la teoria:
MCM pel mètode dels múltiples
MCM pel mètode de les potències
1r) Descomposem els nombres en factors (saber els nombres primers)
2n) Escrivim els nombres en forma de multiplicació de potències
2n) Busquem el m.c.m múltiplicant els números "diferents" de la descomposició factorial, que tenen la potència major.
EXEMPLES:
Problema 2) El veterinari ve al zoo a mirar els goril·les cada 12 dies, les serps cada 15 dies i les taràntules cada 10 dies. Si avui ha vingut i ha mirat els tres animals, quin serà el primer dia que tornarà a venir i podrà veure els goril·les, les serps i les taràntules?
Problema 3) La Júlia va a la muntanya cada 120 dies, la Paula cada 50 dies i la Judith cada 80 dies. Si han coincidit aquest diumenge, quan tornaran a coincidir?
Tema 4.2. Fraccions
Joc de fraccions
Bingo de fraccions:
Saltacavall de fraccions
https://anagarciaazcarate.wordpress.com/2013/05/15/el-salto-de-caballo-de-la-division-de-fracciones/
Fraccions equivalents:
Operar amb fraccions (suma i resta):
Laberintos de fracciones
CÀLCUL
Introducció a les fraccions
Representació gràfica de fraccions.
Font: https://www.unprofesor.com/matematicas/fracciones-propias-o-impropias-1146.html
Font: https://aula05mate.com/aritmetica/numeros-fraccionarios/fracciones/
Fraccions equivalents. Aplificar i simplificar fraccions.
Font: https://www.edufichas.com/matematicas/fracciones/fracciones-equivalentes/
MULTIPLICACIÓ I DIVISIÓ
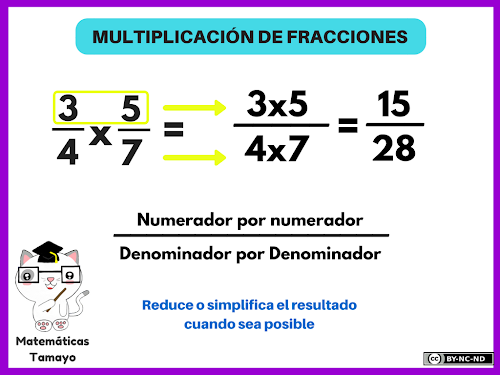
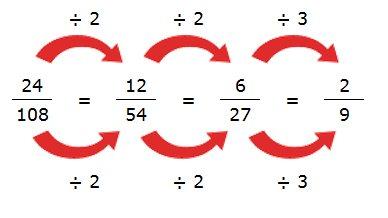
SIMPLIFICAR FRACCIONS
SUMA I RESTA DE FRACCIONS
Previ: Escriu les 3 fraccions amb el mateix denominador i que
siguin equivalents a les inicials.
Exemple 1) 1/12, 2/15, 3/10
1r) Fem l mcm dels denominadors.
mcm (12, 15, 10) = 60
2n) Trobo les fraccions
equivalents. Observo per quina xifra he multiplicat el denominador per obtenir
60 i multiplico el numerador per la mateixa xifra. (Ràpid: 60 : 12 · 1)
1/12, 2/15, 3/10
5 / 60, 8 / 60, 18/60
Exemple 2) 2/10, 5/7, 6/5
Exemple 3) 5/4, 7/6, 1/10
Exemple 1)
Exemple 2)
Exemple 3)
http://www.rena.edu.ve/SegundaEtapa/matematica/swf/mcmMCD.swf
Exercicis per fer amb solucions:
Exercicis amb prodcediment. Nivell alt:
Exercicis de competències bàsiques de fraccions. Clica aquí.
Problemes de fraccions
PASSOS
1r) Dibuixa els quadradets (parts iguals d'una fracció)
2n) Indica el valor del conjunt de "quadradets" i indica quin valor té cada quadradet individualment
3r) Escriu totes les dades i què et demana
4t) Resol el problema indicant el procediment
5è) Resposta amb una frase i unitats
EXEMPLES
1) PROBLEMES DE REPARTIMENT
Problema 1. La Nuri té 240 euros i en dóna 1/6 al Mònica i 2/6 al Jordi. La resta són per 2n d'ESO. Quants diners tindrà cadascú?
Passos 1r, 2n, 3r)
1/6 Mònica 2/6 Jordi 3/6 classe
240/6 = 40€
|
6/6
Total: 240 €
1 quadradet: 240/6= 40 €
|
Cada "rectangle" : 240/6 = 40 €
Quants diners té cadascú?
Pas 4t)
Mònica: 1/6 de 240 = 40 € (ho diu el dibuix)
Jordi : 2/6 de 240 = 40 € · 2 = 80 €
Classe: 3/6 de 240 = 40 € · 3 = 120 €
Pas 5è) Resposta: Mònica té 40 €, Jordi 80 € i la classe 120 €. (tots han de sumar 240!)
Problema 2. L'Àlex té 60 sugus que són 3/8 dels sugus totals. a) Quants sugus hi ha en total? b) La Maria té la resta de sugus, Quants sugus té la Maria? Quina fracció representa els sugus de la Maria?
Passos 1r, 2n, 3r)
Àlex 60 sugus
3/8 5/8 Maria
| 60/3 = 20 |
8/8
1 quadradet: 60/3 = 20 sugos
Total: 20·8 = 160 sugos
|
Cada "rectangle" : 60/3= 20 sugus
Pas 4t)
1/8 són 60/3 = 20 sugus
a) Hi ha 8/8 de sugus. Hi ha 20 · 8 = 160 sugus en total.
b) La Maria té 5/8 que són 20 · 5 = 100 sugus la Maria.
Pas 5è) Resposta: a) Hi ha 160 sugus en total. b) La Maria té 5/8 dels sugus que són 100 sugus. (Els de l'Àlex i la Maria han de sumar 160!)
Problema 3. El Dídac té 21 lacasitos i en dóna 2/7 a la Lucía i 3/7 a l'Anna. La resta els dóna a la professora ;-) Quants lacasitos tindrà cadascú?
Fes els 5 passos.
Problema 4. L'Álex té 46 jocs d'ordinador que són 2/9 dels totals de la col·lecció.a) Quants jocs hi ha en total? b) El Martí té la resta dels jocs. Quants jocs té el Martí? Quina fracció representa els jocs d'ordinador del Martí?
Problema 5. Inventa't un problema que es pugui resoldre amb aquest conjunt de "quadradets".
Problema 6. Inventa't un problema que es pugui resoldre amb aquest conjunt de "quadradets".
2) PROBLEMES ON CAL FER EL M.C.M
Problema 1. El Marc té 1/2 dels caramels, la Clara 1/3 i l'Àlex 1/15, dels 60 caramels totals.
a) Quina és la fracció total de carmels que tenen els tres junts? (suma les fraccions fent el m.c.m dels denominadors).
1/2 + 1/3 + 1/15 = m.c.m (2, 3, 15) = 30
15/30 + 10/30 + 2/30 = 27/30
Resposta: Entre tots tenen 27/30 carmels dels totals.
b) Dibuixa la fracció total amb "quadradets" i indica quant val cada "quadradet".
15/30 Marc 10/30 Clara 2/30 Àlex 3/30 sobren
Fracció 30/30
Cada "quadradet" o sigui 1/30 val: 60/30 = 2 caramels
c) Quina fracció de caramels no té ningú?
Resposta: 3/30
d) Quants caramels té cadasú? Quants caramels sobren?
Resposta:
Marc: 15 quadradets: 2 · 15 = 30 caramels
Clara: 10quadradets: 2 · 10 = 20 caramels
Àlex: 2 quadradets: 2 · 2 = 4 caramels
Sobren: 3 quadradets: 2 · 3 = 6 caramels
(en total han de sumar 60 caramels!!!)
Problema 2. De 72 cromos la Núria en té 1/6, l'Ana 3/8 i el Xavi 1/3.
a) Quina és la fracció total de cromos que tenen els tres junts? (suma les fraccions fent el m.c.m dels denominadors)
1/6 + 3/8 + 1/3 = m.c.m (6, 8, 3) = 24
4/24 + 9/24 + 8/24 = 21/24
Resposta: Entre tots tenen 21/24 carmels dels totals.
b) Dibuixa la fracció total amb "quadradets" i indica quant val cada "quadradet".
Núria 4/24 Ana 9/24 Xavi 8/24 sobren 3/24
Fracció 24/24
Cada "quadradet" o sigui 1/24 val: 72/24 = 3 cromos
c) Quina fracció de cromos no té ningú?
Resposta: 3/24
Resposta:
Núria : 4 quadradets: 3 · 4 = 12 cromos
Ana : 9 quadradets: 3 · 9 = 27 cromos
Xavi: 8 quadradets: 3 · 8 = 24 cromos
Sobren: 3 quadradets: 3· 3 = 9 cromos
(en total han de sumar 72 cromos!!!)
Per practicar:
Inventa't 2 problemes que es puguin resoldre amb aquestes fraccions:
Problema 3.
1/4, 2/5, 1/10
Problema 4.
2/10, 2/5, 1/3
3) PROBLEMES ON ES REPARTEIX 2 VEGADES
Problema 1) La Maria té 600 collarets. En dona 1/3 al Jordi i del que queda, en dona 1/4 a l'Esther. Quants collarets tindrà cadascú? R: Jordi: 200 collarets Esther: 100 collarets Maria : 300 collarets.
Problema 2) El Jordi té 500 cromos. En dóna 2/5 al Marc i del que li queda en dona 2/6 a la Marta. Quants cromos té cadascú? R: Jordi: Marc: 200 cromos Marta:100 collarets Jordi: 200 collarets
Problema 3) El Jan dona 3/5 dels diners a l'Aleix. Del que queda, en dóna 1/4 a l'Anna. Si encara li sobren 15 euros, quants diners s'ha quedat cadascú? R: Jan: 15 euros Anna: 5 euros Aleix: 30 euros.
RESULTATS FRACCIONS COMPETÈNCIES BÀSIQUES
Després de resoldre els problemes de fraccions de CB, fes el següent:
1) Fes 9 multiplicacions amb la calculadora:
a) 3 multiplicacions: positiu · positiu
b) 3 multiplicacions: positiu · nombre entre 0 i 1
c) 3 multiplicacions: nombre entre 0 i 1· nombre entre 0 i 1
Resol: En quins casos a) , b), c), el resultat final de la multiplicació és menor que alguna de les xifres de l'enunciat?
2) Inventa't 3 problemes semblants als treballats a classe. Resol-los amb el procediment i fent una frase com a resultat final.
Tema 5. Proporcionalitat i percentatges
Jocs matemàtics:
Proporcionalitat:
Tot: https://www.edu.xunta.gal/centros/iesagraleboris/system/files/solucionario2.pdf
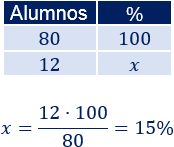
Percentatges
Percentatge d'una quantitat
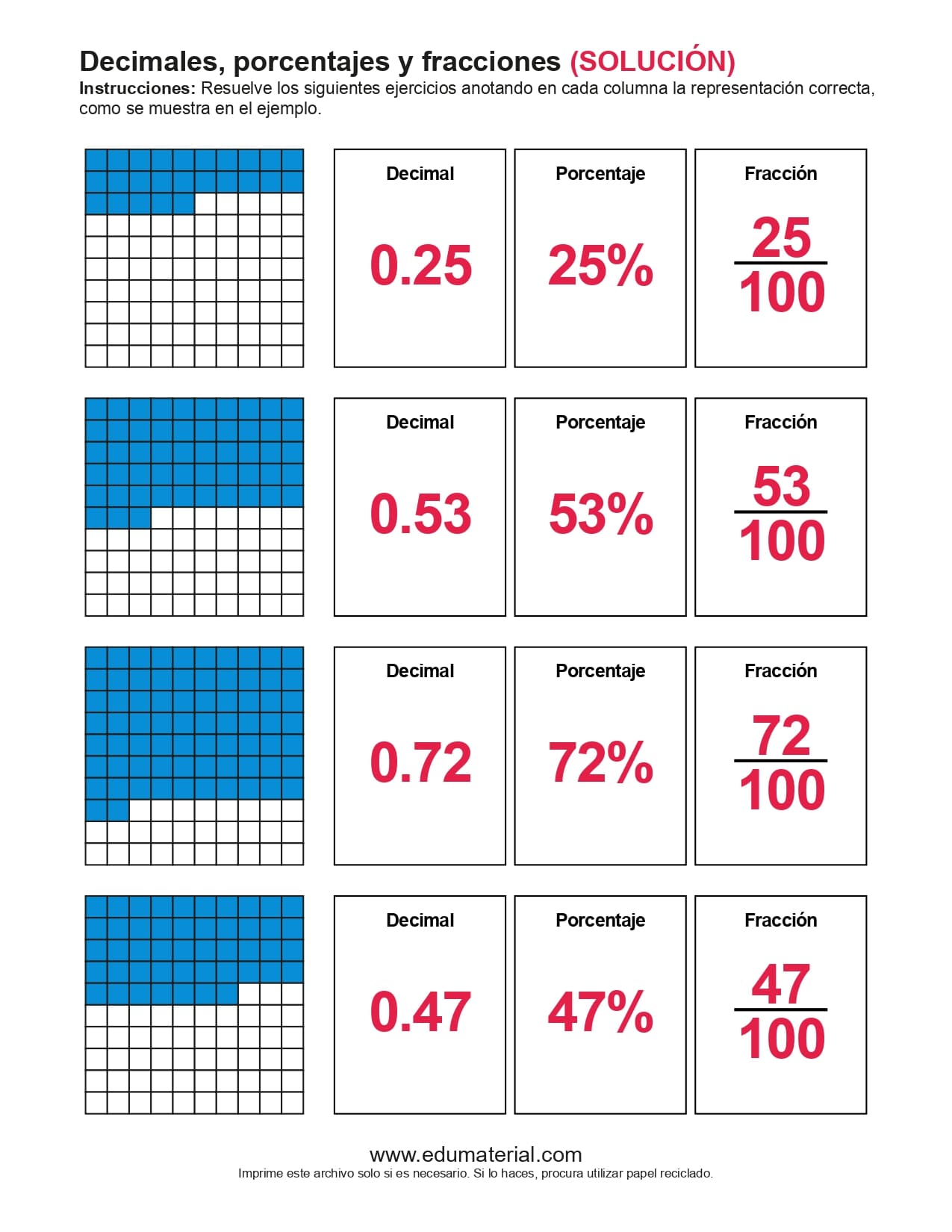
Percentatge, decimal, fracció
Font: https://edumaterial.com/wp-content/uploads/2021/02/000075-Fracciones-Decimales-Porcentajes-Set-1-EduMaterial_page-0004.jpg
https://www.cerebriti.com/juegos-de-matematicas/calculo-y-porcentajes
https://www.cajondeciencias.com/Descargas%20mate1/ER%20porcentajes%202.pdf
Bingo: https://anagarciaazcarate.wordpress.com/2011/03/04/bingo-de-porcentajes/
